ก่อนอื่นเราต้องมี python 3.6+ มาก่อน เพราะว่ายังหาวิธีดึงข้อมูลด้วย matlab ไม่เป็น 555 หลังจากนั้นก็ลง pandas_datareader module ใน command prompt ด้วยคำสั่ง
pip install pandas-datareader
import pandas_datareader as pdr import pandas as pd import datetime pttgc = pdr.get_data_yahoo('PTTGC.BK', start=datetime.datetime(2020, 1, 1), end=datetime.datetime(2020, 7, 24)) df = pd.DataFrame(pttgc) df.to_csv (r'E:\backupusb\myMATLAB\export_pttgc.csv', header=True) print(df)
เมื่อทำการเซฟข้อมูลลงเครื่องเรียบร้อย เราก็มาทำการplotใน MATLAB ได้
ถามว่าทำไมถึงไม่ใช้pythonทำ...คำตอบง่ายมาก "ก็สะดวก MATLAB กว่า" นั่นเอง 5555
เอ้า เปิด MATLAB ขึ้นมาแล้วพิมพ์คำสั่งไปตามนี้
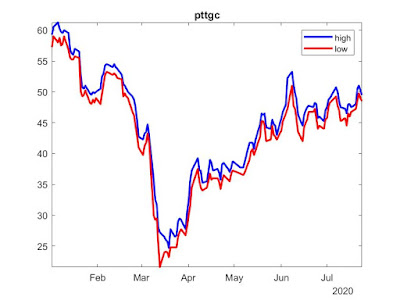
clear; filename = 'export_pttgc.csv'; [num,txt,raw] = xlsread(filename); %Date|High|Low|Open|Close|Volume|Adjust close hi = num(:,1); lo = num(:,2); op = num(:,3); cl = num(:,4); vol = num(:,5); adjcl = num(:,6); time = datetime(txt(2:end,1),'InputFormat','MM/dd/yyyy'); plot(time,hi,'-b','LineWidth',2); hold on; plot(time,lo,'-r','LineWidth',2); legend('high','low'); axis tight;hold off; title('pttgc')
เราก็จะได้กราฟสวยมาเริ่มเล่นใน episode ต่อไป ...
ตอนนี้ขอตัวไปเรียนการวิเคราะห์หุ้นแบบ technical ก่อน มีอะไรใหม่เดี๋ยวจะมาอัพเดทให้